Many aspects of modern applied research rely on a crucial algorithm called gradient descent. This is a procedure generally used for finding the largest or smallest values of a particular mathematical function—a process known as optimizing the function. It can be used to calculate anything from the most profitable way to manufacture a product to the best way to assign shifts to workers.
Yet despite this widespread usefulness, researchers have never fully understood which situations the algorithm struggles with most. Now, new work explains it, establishing that gradient descent, at heart, tackles a fundamentally difficult computational problem. The new result places limits on the type of performance researchers can expect from the technique in particular applications. Paul Goldberg of the University of Oxford, co-author of the work along with John Fearnley and Rahul Savani of the University of Liverpool and Alexandros Hollender of Oxford commented:
“There is a kind of worst-case hardness to it that is worth knowing about.”
You can imagine a function as a landscape, where the elevation of the land is equal to the value of the function at that particular spot. Gradient descent searches for the function’s local minimum by looking for the direction of the steepest ascent at a given location and searching downhill away from it. The slope of the landscape is called the gradient, hence the name gradient descent.
Gradient descent is an essential tool of modern applied research, but there are many common problems for which it does not work well. But before this research, there was no comprehensive understanding of exactly what makes gradient descent struggle and when—questions in another area of computer science known as computational complexity theory helped to answer. Costis Daskalakis of the Massachusetts Institute of Technology also commented:
“A lot of the work in gradient descent was not talking with complexity theory.”
Computational complexity is the study of the resources, often computation time, required to solve or verify the solutions to different computing problems. Researchers sort problems into different classes, with all problems in the same class sharing some fundamental computational characteristics.
To take an example imagine a town where there are more people than houses and everyone lives in a house. You’re given a phone book with the names and addresses of everyone in town, and you’re asked to find two people who live in the same house. You know you can find an answer because there are more people than houses, but it may take some looking.
This question belongs to a complexity class called TFNP, short for “total function non-deterministic polynomial.” It is the collection of all computational problems that are guaranteed to have solutions and whose solutions can be checked for correctness quickly. The researchers focused on the intersection of two subsets of problems within TFNP.
The first subset is called PLS (polynomial local search). This is a collection of problems that involve finding the minimum or
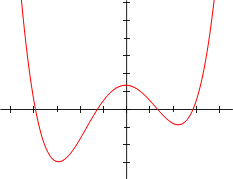
One problem that falls into the PLS category is the task of planning a route that allows you to visit some fixed number of cities with the shortest travel distance possible given that you can only ever change the trip by switching the order of any pair of consecutive cities in the tour. It’s easy to calculate the length of any proposed route and, with a limit on the ways you can tweak the itinerary, it’s easy to see which changes shorten the trip. You’re guaranteed to eventually find a route you can’t improve with an acceptable move—a local minimum.
The second subset of problems is PPAD (polynomial parity arguments on directed graphs). These problems have solutions that emerge from a more complicated process called Brouwer’s fixed point theorem. The theorem says that for any continuous function, there is guaranteed to be one point that the function leaves unchanged—a fixed point, as it’s known. This is true in daily life. If you stir a glass of water, the theorem guarantees that there absolutely must be one particle of water that will end up in the same place it started from.
The intersection of the PLS and PPAD classes itself forms a class of problems known as PLS int PPAD. It contains many natural problems relevant to complexity researchers. However, until now, researchers were unable to find a natural problem that’s complete for PLS int PPAD—meaning that it is an example of the hardest possible problems that fall within the class.
Prior to this paper, the only known PLS int PPAD-complete problem was a rather artificial construction—a problem sometimes called “Either-Solution.” This problem glued together with a complete problem from PLS and a complete problem from PPAD, forming something a researcher would be unlikely to encounter outside this context. In the new paper, the researchers proved that gradient descent is as hard as Either-Solution, making gradient descent itself PLS int PPAD-complete. None of this means that gradient descent will always struggle. In fact, it’s just as fast and effective as ever for most uses. Goldberg also said:
“There’s a slightly humorous stereotype about computational complexity that says what we often end up doing is taking a problem that is solved a lot of the time in practice and proving that it’s actually very difficult.”
But the result does mean applied researchers shouldn’t expect gradient descent to provide precise solutions for some problems where precision is important.
The question of precision speaks to the central concern of computational complexity—the evaluation of resource requirements. There is a fundamental link between precision and speed in many complex questions. For an algorithm to be considered efficient, you must be able to increase the precision of a solution without paying a correspondingly high price in the amount of time it takes to find that solution. The net result means that for applications that require very precise solutions, gradient descent might not be a workable approach.
For example, gradient descent is often used in machine learning in ways that don’t require extreme precision. But a machine learning researcher might want to double the precision of an experiment. In that case, the new result implies that they might have to quadruple the running time of their gradient descent algorithm. That’s not ideal, but it is not a deal-breaker.
But for other applications, like in numerical analysis, researchers might need to square their precision. To achieve such an improvement, they might have to square the running time of gradient descent, making the calculation completely intractable. They must, and in practice do compromise somewhere. They either accept a less precise solution, limit themselves to slightly easier problems, or find a way to manage an unwieldy runtime.
But this is not to say a fast algorithm for gradient descent doesn’t exist. It might. But the result does mean that any such algorithm would immediately imply the existence of fast algorithms for all other problems in PLS int PPAD—a much higher bar than merely finding a fast algorithm for gradient descent itself.